الدرس الثالث في الكهرباء التذبذبات الحرة في دارة RLC
في دارة تتكون من موصل أومي R ومكثف C ووشيعة ومولد للتور المستمر قابل للضبط، وبعد شحن المكثف، نقوم بأرجحة قاطع التيار إلى الموضع (2) (أنظر الشكل أسفله) هذا يؤدي إلى تفريغ المكثف المشحون في وشيعة الدارة إلى ظهور ذبذبات
حرة ومخمذة. تنعت هذه التذبذبات بالحرة، وذلك لعدم توفر الدارة RLC المتوالية على أي مصدر أخر للطاقة ماعدا الطاقة التي يخزنها المكثف.
يمكن راسم التذبذب الذاكرتي من معاينة تغيرات التوتر بين مربطبي المكثف خلال عملية التفريغ.
نظام حرج : في التذبذبات الحرة توجد قيمة معينة للمقاومة نرمز لها ل Re وتسمى مقاومة حرجة. وهي مقاومة تفصل بين النظام الشبه الدوري والنظام اللادوري. في هذا النظام يرجع التوتر بين مربطي المكثف إلى الصفر بسرعة وبدون تذبذب. (أنظر الشكل أسفله) وتجدر الإشارة إلى أن Re تتعلق بقيمتي L وC.
نعتبر الدارة الممثلة في الشكل جانبه والمكونة من مكثف سعته C، ووشيعة معمل تحريضها الذاتي L ومقاومتها منعدمة. نسمي هذه الدارة بالمثالية لإستحالة تحقيقها تجريبيا نظرا لتوفر الوشيعات على مقاومة داخلية ناتجة عن أسلاك لفاتها، أضف إلى ذلك مقاومة أسلاك الربط.
حرة ومخمذة. تنعت هذه التذبذبات بالحرة، وذلك لعدم توفر الدارة RLC المتوالية على أي مصدر أخر للطاقة ماعدا الطاقة التي يخزنها المكثف.
يمكن راسم التذبذب الذاكرتي من معاينة تغيرات التوتر بين مربطبي المكثف خلال عملية التفريغ.
أنظمة الذبذبات الحرة:
نظام شبه دوري : نظام يحدث فقط إذا كانت قيمة المقاومة R صغيرة، حيث نحصل في هذه الحالة على ذبذبات يتناقص وسعها تدريجيا مع الزمن مثل الذي في الشكل : |
| نظام شبه دوري-المقاومة ضعيفة |
نظام لادوري : عندما تكون المقاومة R كبيرة جدا تزول التذبذبات، نظرا لوجود خمود مهم أنظر الشكل :
 |
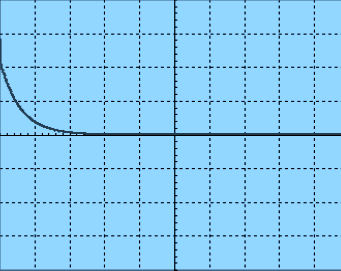| نظام لادوري-المقاومة كبيرة |
 |
| نظام حرج |
خلاصة : تمكننا قيم المقاومة R للدارة RLC من التمييز بين الأنظمة الثلاثة: شبه دوري والحرج واللادوري، وبالنسبة للنظام شبه الدوري، لا يتعلق الدور T بالمقاومة.
ملحوظات:
-التوتر Uc بين مربطي المكثف متناوب، أي أنه يتأرجح من قيم قصوى موجبة وقيم دنيا سالبة، لهذا نقول أن تفريغ المكثف تذبذبي.
-يتناقص وسع التوتر Uc مع مرور الزمن، إذا نقول أن التذبذبات مخمذة.
-يؤدي تفريغ مكثف مشحون في دارة RLC متوالية إلى ظهور تذبذبات حرة مخمذة. نقول إذا إن الدارة RLC المتوالية عبارة عن متذبذب كهربائي.
الذبذبات غير المخمدة في دارة مثالية LC:
نعتبر الدارة الممثلة في الشكل جانبه والمكونة من مكثف سعته C، ووشيعة معمل تحريضها الذاتي L ومقاومتها منعدمة. نسمي هذه الدارة بالمثالية لإستحالة تحقيقها تجريبيا نظرا لتوفر الوشيعات على مقاومة داخلية ناتجة عن أسلاك لفاتها، أضف إلى ذلك مقاومة أسلاك الربط.
خلال التذبذبات الكهربائية الحرة غير المخمدة لدارة LC، يحقق التوتر Uc بين مربطي المكثف المعادلة التفاضلية التالية:
d²Uc/dt+ 1/LC*Uc =0
يمكننا تعويض Uc ب q/C نجد المعادلة التفاضلية، التي تحققها الشحنة الكهربائية q :
d²q/dt² + 1/LC*q = 0
يمكنك التعرف أكثر عن المعادلات الأخرى بتحميلك للملف المرفق.
إشترك ليصلك جديد الدروس والمواضيع!
الأكثر تصفحا هذا الأسبوع
-
تحليل نص كلود برنارد تأطير النص: يتأطر النص ضمن مجزوءة المعرفة المرتبطة بالإنسان بإعتباره كائن عارف ومنتج لأفكار تمكنه من معرفة ح... -
تأطير النص: يتأطر النص ضمن مجزوءة الوضع البشري وينفتح مضمونه على مفهوم الغير بإعتباره الشبيه لي والمختلف عني في نفس الوقت وبالضبط فهو يع... -
إشكال النص: إذا كان الإنسان كائنا عارفا، فعلى أي أساس تقوم المعرفة العلمية؟ هل يمكن أن تقوم على العقل فقط أم على التجربة فقط أم على العقل وا... -
.png)
السلام عليكم ورحمة الله وبركاته متابعي مدونة 3elmo السلسلة المشهورة والقوية والمحبوبة لدى التلاميذ سلسلة ديما ديما لمادة الرياضيات الخ... -
المحور الثاني : معرفة الغير السؤال الإشكالي المحوري: هل يمكننا معرفة الغير؟ وما هو المجال الذي يمكن أن يتحقق فيه ذلك؟ وماهي الادوات الم... -
بسم الله الرحمن الرحيم السلام عليكم ورحمة الله وبركاته أقدم لكم برنام Guide Des Automatismes الإصدار 7 هذا البرنامج عبارة عن م... -
التقديم والإشكالات موقف الفيلسوف مارتن هايدغر: يقدم الفيلسوف الألماني تصوره حول وجود الغير ومعنى الوجود الإنساني في العالم، ب... -
السلام عليكم ورحمة الله وبركاته متابعي مدونة 3elmo أضع بين أيديكم هذا الكتاب الرائع لملخصات مركزة لقواعد مادة الرياضيات بالنسبة لشعبة... -
مفاهيم: الحرية : هي عدم الخضوع لأي قيد أو شرط أي التصرف وفق ما تمليه الذات على نفسها وبدون أي إكراه، سواء أكان داخليا او خارجيا. -
.png)
تحميل سلسلة 20/20 مادة الرياضيات الجزء الأول [PDF] تحميل كتاب أو سلسلة 20/20 مادة الرياضيات لجميع الشعب (العلوم التجريبية جميع المس...
0 comments:
إرسال تعليق